
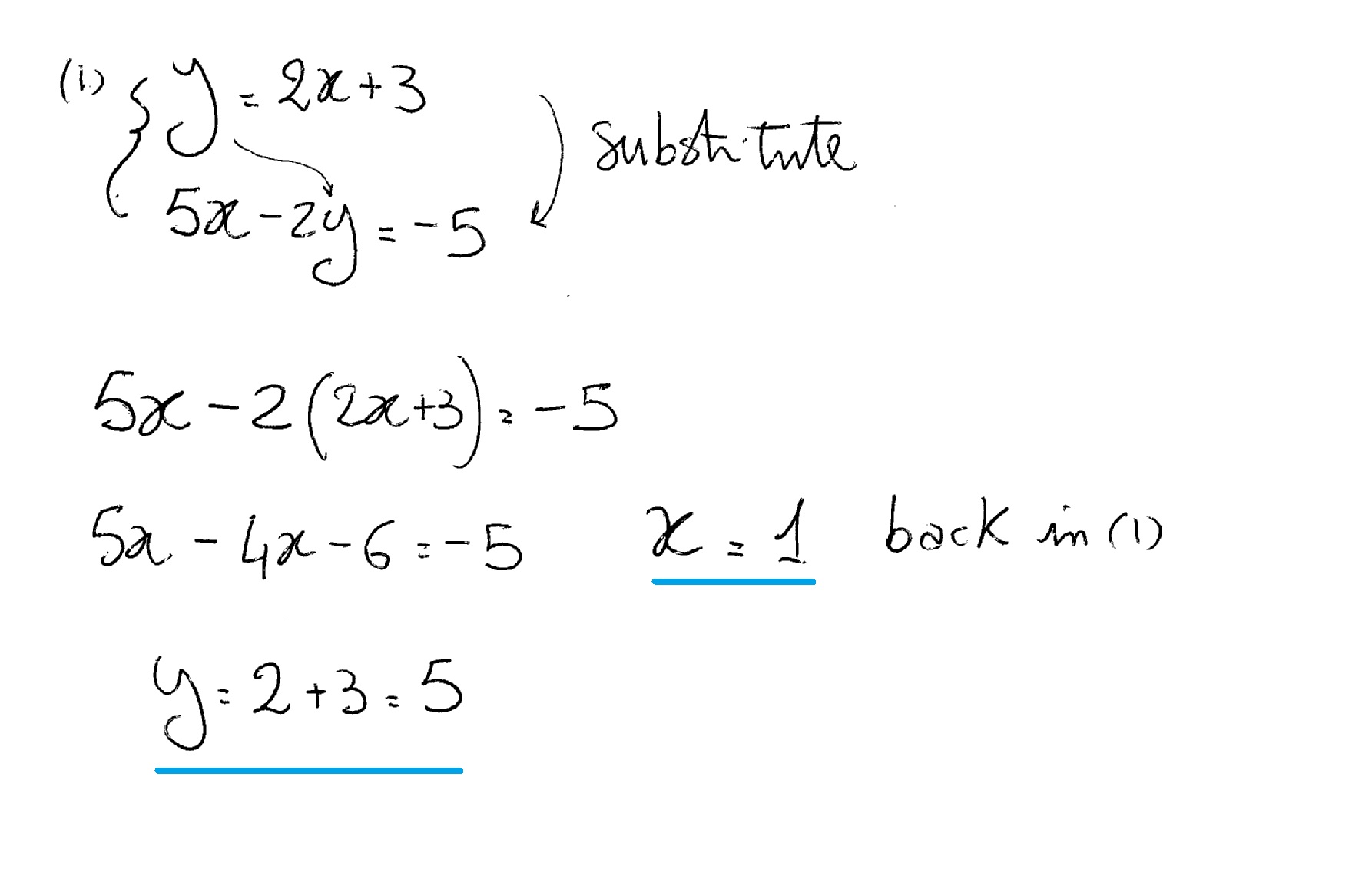
In some instances, we are going to need to do some simplification of both equations before we can carry on with substitution and solving. The following image below summarizes the work we've just done: Let's chose the first equation because it is more simple. Now that we have x, we can put x=7 into either of the equations to solve for y. Now that we have successfully performed substitution, let's solve for x. Now, we are going to substitute our newly rearranged equation 6x - 7 = y into -9x + 2y = 7. Step 2: Substitute the rearranged equation into its partner We could certainly take the second equation, but that would involve more work. Let's use the first equation and rearrange it so we can have y by itself. Take the following simultaneous equations and solve.
#Solve by substitution how to#
The best way to learn and master how to solve by substitution is to do some practice problems. It doesn't matter which variable you solve first, just note that x is often the easier one to solve for first, as it often involves less modification in the initial give equations. Also note that in this example we chose to solve for x first. Step 5: Write final answer out as a point Once we have the value for x, we can substitute it into any of the two equations to find our solution for y. Step 4: Substitute the solution for x into either of the initially given equations to find y But note all we have to do is get x by itself. Since this is just a general case, we can't solve for x.

Step 1: Rearrange one of the equations to get 'y' by itselfġ) y = a x t y = \frac) = x + b z ( t a x ) = x + b This procedure is better outlined below with the general example:Ĭonsider the following equations, with (x,y) being coordinates and everything else representing constants. The basic procedure behind solving systems via substitution is simple: Given two linear equations, all we need to do is to "substitute" one in the pair of equations into its other by rearranging for variables. Now that we've covered the basics, let's solve systems using substitution! Solving Systems of Equations By Substitution:īefore we get into using the method of substitution, make sure you're comfortable with your algebra by reviewing the lesson on solving linear equations with variables on both sides. To make sure you're ready for elimination, it is important to master adding and subtracting polynomials and adding and subtracting rational expressions. For elimination, please check out the video and articles that focus on that method in particular. In this article, we will focus on substitution, which is arguably slightly more simple than the other method, elimination. To do so, there are two main methods: solving systems by substitution, and solving systems by elimination. We also have graphing systems of equations and inequalities covered! We have the specific lessons on how to determine the number of solutions to linear equations and system of linear-quadratic equations. In a system of equations, there are several outcomes which can occur with regards to the number of solutions. Further information on system of equations can be founded in another lesson. In solving systems of equations, what we are trying to do is trying to find values of x and y that makes two distinct equations equal to each other – effectively "solving" both equations. In the case of systems of equations, the process isn't that different. Then, the next natural step is to solve this equation using algebra, giving us the "solution" that x = 1. With that knowledge, since y is equal to both 2x and 2, we can say that 2x = 2. In this example equation, we know that y is equal to 2x and is also equal to 2. Take for example the following, simple, equation: y = 2x = 2 When we say "solve", with regards to linear, quadratic, exponential, or any other type of equation, what we really mean is that we are trying to find values of 'x' – the dependent variable – that satisfy 'y' – the independent variable. Before we get into solving systems of linear equations via the substitution method, let's first consider and understand what it means to "solve" a system of equations.


 0 kommentar(er)
0 kommentar(er)
